| - Home - Screen Shots - Manuals - Downloads - Developers - | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
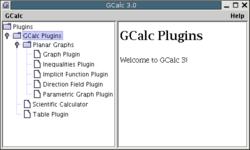
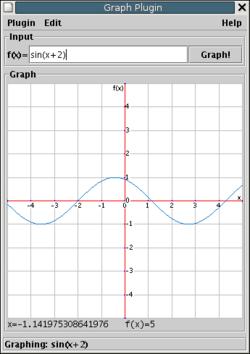
GCalc 3 Manual1. Quick TutorialRunning the applicationAssuming that Java 1.4 is installed on your computer, you can start GCalc 3 by clicking on the button labeled, "GCalc 3 Beta". If you do not have Java 1.4 (or higher) installed, please do that now. First ImpressionWhen you launch GCalc 3, the interface shown (Figure 1) will show up. On the right, there is a list of plugins that is available. As you browse through the list, the description on the right will change. Starting a pluginSelect the plugin you want to start. Double click on its name which is displayed on the left side of the main screen. Then the plugin window should come up. For the rest of the tutorial, let's assume that we started the Graph Plugin. Graph PluginTo graph a function, type in the desired function into the Input section of the window at the top of the window. Notice that you only need to put in the 'left-hand side' of the function definition since the right hand side 'f(x)=' is already provided. The following examples are valid inputs:
When ready, click on the Graph! button. Or more directly, press enter. If the input is well-formed, a color will be picked and the graph of the function will be shown on the Graph screen. 2. FunctionTerminologyIn the following sections, unary means that the function takes one argument. Unless noted otherwise, unary functions have the general form Constants & VariablesTo GCalc, any consecutive string of alphabetic characters that isn't a function name is a variable name. GCalc 3 is case sensitive (unlike GCalc 2). The most common variable name is There are currently two reserved variables names Arithmetic
These are the 5 basic functions of arithmetic. Standard order of operations apply, i.e. Exponentiation, then multiplication and division, then addition and subtraction. Exponentiation is right associative while the rest are left-associative. This means that Trigonometric
These are the trignometric functions (and their inverses) found in any self-respecting pre-calculus textbook. Angles are always expressed in radians. Hyperbolic Functions
These are the hyperbolic functions (and their inverses) found in any self-respecting calculus textbook. Sign Functions
These are unary functions which deal with the sign of the given argument. The expressions Roots
Exponential/Logarithm
Finally, Engineering
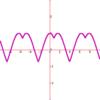
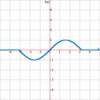
Each of the three wave functions ( Each of the three pulse functions ( Step function is also known as the Heavyside function. Finally the stair function Rounding
The rounding function, Maximum and Minimum
Sum and Product
Calculus
Given a function Equality/Inequality Operations
These operations take two numbers and does a comparison. If the inequality or equality evaluates to true, then the operation returns Boolean Operations
These standard logical operation take inequalities or other boolean operations as arguments. The operation
is a valid expression.
Be sure to use parentheses with Piecewise Function
With For example, 3. Graph PluginsThis section contains features that are common to the 2D graph plugins. Currently, there are 6 graph plugins. In addition to the vanilla 2D Cartesian plane graphing, there are plugins for:
OverviewGraph plugins share a similar GUI (Graphical User Interface). The window is split into two boxes. The lower one contains the graph, and the upper one input interface. The window also features the menu bar (above, usually) and the status bar beneath. Hiding the pluginGCalc comes with a myriad of plugins. If you ever wish to make one invisible, you can select Hide Plugin from the Plugin menu. The state of the plugin will persists until you quit GCalc. Starting the plugin again while GCalc is still running will restore the state of the plugin. PrintingPrinting is an experimental feature that will print the current graph. To graph Select the Print... option under the Plugin menu. You will be asked to provide a dot-per-inch parameter, the default is 72 dots-per-inch, which approximately corresponds to most computer screens. But most printers are able to print 300 dots-per-inch or more. Of course, greater the dots-per-inch, smaller the graph. After that you will see a standard interface for printing. This might be system dependent.Other featuresMore to come... 4. System RequirementsHardwareThere are no formal hardware requirements. Since GCalc is built on Java technology, it is cross-platform. Anywhere that Java runs, GCalc should work also. GCalc 3 does work on a Pentium II 300 MHz machine that I have with 128 MB RAM. I would suggest that people have at least 128 MB RAM, especially if you use the more intensive plugins. With computers you buy these days, this shouldn't be a problem. GCalc 3 is developed on Eclipse 3.0, running on Gentoo Linux running on a Celeron 2.4 with 512 MB RAM. The machine's name is Fantine. SoftwareGCalc 3 is developed using Java 1.4. You should have Java 1.4 (or higher) installed on your machine. Although not strictly necessary, a web browser is helpful. (Firefox, Internet Explorer, Safari, and others are viable options.) This is subject to change without notice. (I might switch to Java 1.5.) UserThe user must have the willingness to think critically about what GCalc is doing. If you're the type to shut of your brain while graphing, this is not the tool for you. As it's often said, do not operate heavy (graphing) machinery...
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| © Copyright 2015 Jiho Kim | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
About GCalc Support GCalc Acknowledgement