GCalc.net: Free Online Graphing Calculator

GCalc 3 Manual

1. Quick Tutorial

Running the application

Assuming that Java 1.4 is installed on your computer, you can start GCalc 3 by clicking on the button labeled, "GCalc 3 Beta". If you do not have Java 1.4 (or higher) installed, please do that now.

First Impression

(Figure 1)

When you launch GCalc 3, the interface shown (Figure 1) will show up. On the right, there is a list of plugins that is available. As you browse through the list, the description on the right will change.

Starting a plugin

Select the plugin you want to start. Double click on its name which is displayed on the left side of the main screen. Then the plugin window should come up.

For the rest of the tutorial, let's assume that we started the Graph Plugin.

Graph Plugin

(Figure 2)

To graph a function, type in the desired function into the Input section of the window at the top of the window. Notice that you only need to put in the 'left-hand side' of the function definition since the right hand side 'f(x)=' is already provided. The following examples are valid inputs:

-4 constant
2x-1 linear
x^2+3*x+2 quadratic
(x+2)^3-2x polynomial
(x^2+3x+2)/(x-1) rational
e^(-x) exponential
sin(x+2) trigonometric
sin(pi x)+e^x-(x+1)^3 mixed

For a more detailed description of available functions can be found in later section.

When ready, click on the Graph! button. Or more directly, press enter. If the input is well-formed, a color will be picked and the graph of the function will be shown on the Graph screen.

2. Function

Terminology

In the following sections, unary means that the function takes one argument. Unless noted otherwise, unary functions have the general form function(x). Binary, tertiary, and multi-ary functions are natural extensions of this idea, each having two, three and more than two arguments respectively.

Binary infix operations are functions which take two arguments on either side of the function name.

Constants & Variables

To GCalc, any consecutive string of alphabetic characters that isn't a function name is a variable name. GCalc 3 is case sensitive (unlike GCalc 2).

The most common variable name is x, but you may have the occasion to use others, such as y, z, t, or r, or even pIzzA.

There are currently two reserved variables names pi and e, which represent the numbers 3.14159265... and 2.7182818..., respectively.

Arithmetic

`+`	Addition
`-`	Subtraction

`*`	Multiplication
`/`	Division

`^`	Exponentiation

These are the 5 basic functions of arithmetic. Standard order of operations apply, i.e. Exponentiation, then multiplication and division, then addition and subtraction.

Exponentiation is right associative while the rest are left-associative. This means that x^y^z is the same as x^(y^z) while a+b+c is equivalent to (a+b)+c.

Trigonometric

`sin`	Sine
`cos`	Cosine
`tan`	Tangent
`csc`	Cosecant
`sec`	Secant
`cot`	Cotangent

`asin`	Arcsine
`acos`	Arccosine
`atan`	Arctangent
`acsc`	Arccosecant
`asec`	Arcsecant
`acot`	Arccotangent

These are the trignometric functions (and their inverses) found in any self-respecting pre-calculus textbook. Angles are always expressed in radians.

Hyperbolic Functions

`sinh`	Hyperbolic Sine
`cosh`	Hyperbolic Cosine
`tanh`	Hyperbolic Tangent
`csch`	Hyperbolic Cosecant
`sech`	Hyperbolic Secant
`coth`	Hyperbolic Cotangent

`asinh`	Hyperbolic ArcSine
`acosh`	Hyperbolic ArcCosine
`atanh`	Hyperbolic ArcTangent
`acsch`	Hyperbolic ArcCosecant
`asech`	Hyperbolic ArcSecant
`acoth`	Hyperbolic ArcCotangent

These are the hyperbolic functions (and their inverses) found in any self-respecting calculus textbook.

Sign Functions

`-`	Negation
`neg`	Negation
`abs`	Absolute Value
`sgn`	Sign

These are unary functions which deal with the sign of the given argument. The expressions -x and neg(x) are equivalent way to express the negation of x. The expression abs(x) is the absolute value of x. The expression sgn(x) is 1 if x>0, -1 if x<0, and 0 if x=0.

Roots

`sqrt`	Square Root
`root`	n^th Root

sqrt is a unary function that evaluates the the square root of the argument.

root is a binary function that calculates the n^th root. The general format is root(x, n), where n is an integer. This is preferred to x^(1/n) since you'll notice that if n is odd, the x^(1/n) is undefined for negative x.

Exponential/Logarithm

`exp`	Exponential
`log`	Common Logarithm
`ln`	Natural Logarithm
`logb`	Log base b

exp is a unary function that evaluates the the exponential of the argument. It is equivalent to e^x.

log and ln are unary functions that evaluate the the common and natural logarithm of the argument.

Finally, logb(x,b) evaluates the logarithm base b of x. It is mathematically equivalent to log(x)/log(b) and ln(x)/ln(b). Conversely log(x) and ln(x) are equivalent to logb(x,10) and logb(x,e), respectively.

Engineering

`sqwave`	Square Wave
`trwave`	Triangle Wave
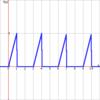
`swwave`	Sawtooth Wave

`sqpulse`	Square Pulse
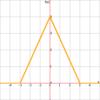
`trpulse`	Triangle Pulse
`swpulse`	Sawtooth Pulse

`step`	Step
`stair`	Stair

(Figure 3)

(Figure 4)

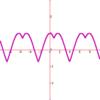
Each of the three wave functions (sqwave, trwave, and swwave) take three arguments. The general format is XXwave(t,d,T), where t is a time function, 0<d<1 is the duty cycle, and T is the period. For example, sqwave(x,1/3,3) will produce the graph shown (Figure 3).

Each of the three pulse functions (sqpulse, trpulse, and swpulse) take two arguments. The general format is XXpulse(t,a), where t is a time function. The pulse will 'turn on' at t=0 and 'turn off' at t=a. For example, 4 trpulse(t+3,6) will produce the graph shown (Figure 4).

Step function is also known as the Heavyside function. step(x) is 1 if x is positive, and 0 otherwise.

Finally the stair function stair(x,a) is 0 when x is negative. There is a rise of 1 (starting at x=0) and a run of a.

Rounding

`ceil`	Ceiling
`floor`	Floor

The rounding function, ceil and floor are both unary functions which return a rounded value of the argument. ceil(x) is the smallest (closest to negative infinity) integer that is not greater than x. Similarly, floor(x) is the largest (closest to positive infinity) integer that is not less than x.

Maximum and Minimum

(Figure 5)

`max`	Maximum
`min`	Minimum

max and min are multi-ary functions which respectively compute the maximum and minimum of the given parameters. For example max(cos(x),sin(x)) will generate the graph shown (Figure 5). Both max and min can take many inputs.

Sum and Product

`sum`	Sum
`prod`	Product

sum and prod are multi-ary functions which respectively compute the sum and product of the given parameters. For example sum(1,-2x,x^2) is equivalent to 1-2x+x^2. Both these functions can take many inputs.

Calculus

`diff`	Differentiation
`int`	Numerical Integration
`taylor`	Taylor Series Approximation

diff has the format diff(f,x), where the first argument is a multivariable function. Differentiation is always with respect to some variable, which is named in the other argument of diff. One can also name multiple variables, to take multiple derivatives with respect to those variables. For example, diff(x^2 y^2, x, y) will be the same as 4x*y.

int has the general format int(f,x,a,b,tol), where

f is a function of one variable,
x is variable of integration,
a and b are the lower and upper end point, respectively, and
tol is the tolerance of the numerical integration algorithm.

GCalc utilizes an adaptive Simpson's rule algorithm for numerical integration. Be careful when integrating nonsmooth or discontinuous functions.

Given a function f with independent variable x, the taylor polynomial approximation of f of degree n at x0 can be found with taylor(f,x0,n).

Equality/Inequality Operations

`==`	Equals
`<>`	Not Equals
`>=`	Greater than or equal
`>`	Greater than
`<=`	Less than or equal
`<`	Less than

These operations take two numbers and does a comparison. If the inequality or equality evaluates to true, then the operation returns 1. Otherwise, the operation returns a NaN (Not A Number).

Boolean Operations

`not`	Logical Negation ('not')
`&&`	Conjunction ('and')
`\|\|`	Disjunction ('or')

These standard logical operation take inequalities or other boolean operations as arguments. The operation not is unary, while && and || are (infix) binary. For example,

not(x>1 && x<=y)

is a valid expression.

Be sure to use parentheses with not to minimize confusion about order of precedence.

Piecewise Function

case Case

(Figure 6)

With case, one can define a piecewise function. The general format is case(t1,v1,t2,v2,...,[default]). If the test tN evaluates to true, then the function value is the value vN at that point. At any given point, if multiple tests evaluate to true, then the function value is the value corresponding to the first test that evaluates to true. If no test evaluates to true, then either the function takes on the optional default or is undefined.

For example, case(x^2<=pi^2,sin(x),0) corresponds to the graph shown (Figure 6).

3. Graph Plugins

This section contains features that are common to the 2D graph plugins. Currently, there are 6 graph plugins. In addition to the vanilla 2D Cartesian plane graphing, there are plugins for:

Inequalities
Implicit Functions
Direction Fields
Polar Graphs
Parametric Graphs

We'll get into the specifics of each plugin later, but first, we begin with a broad overview.

Overview

(Figure 7)

Graph plugins share a similar GUI (Graphical User Interface). The window is split into two boxes. The lower one contains the graph, and the upper one input interface. The window also features the menu bar (above, usually) and the status bar beneath.

Hiding the plugin

GCalc comes with a myriad of plugins. If you ever wish to make one invisible, you can select Hide Plugin from the Plugin menu. The state of the plugin will persists until you quit GCalc. Starting the plugin again while GCalc is still running will restore the state of the plugin.

Printing

Printing is an experimental feature that will print the current graph. To graph Select the Print... option under the Plugin menu. You will be asked to provide a dot-per-inch parameter, the default is 72 dots-per-inch, which approximately corresponds to most computer screens. But most printers are able to print 300 dots-per-inch or more. Of course, greater the dots-per-inch, smaller the graph.

After that you will see a standard interface for printing. This might be system dependent.

Other features

More to come...

4. System Requirements

Hardware

There are no formal hardware requirements. Since GCalc is built on Java technology, it is cross-platform. Anywhere that Java runs, GCalc should work also.

GCalc 3 does work on a Pentium II 300 MHz machine that I have with 128 MB RAM. I would suggest that people have at least 128 MB RAM, especially if you use the more intensive plugins. With computers you buy these days, this shouldn't be a problem.

GCalc 3 is developed on Eclipse 3.0, running on Gentoo Linux running on a Celeron 2.4 with 512 MB RAM. The machine's name is Fantine.

Software

GCalc 3 is developed using Java 1.4. You should have Java 1.4 (or higher) installed on your machine.

Although not strictly necessary, a web browser is helpful. (Firefox, Internet Explorer, Safari, and others are viable options.)

This is subject to change without notice. (I might switch to Java 1.5.)

User

The user must have the willingness to think critically about what GCalc is doing. If you're the type to shut of your brain while graphing, this is not the tool for you. As it's often said, do not operate heavy (graphing) machinery...