2. Function
Terminology
In the following sections, unary means that the function takes one argument. Unless noted otherwise, unary functions have the general form function(x). Binary, tertiary, and multi-ary functions are natural extensions of this idea, each having two, three and more than two arguments respectively.
Binary infix operations are functions which take two arguments on either side of the function name.
Constants & Variables
To GCalc, any consecutive string of alphabetic characters that isn't a function name is a variable name. GCalc 3 is case sensitive (unlike GCalc 2).
The most common variable name is x, but you may have the occasion to use others, such as y, z, t, or r, or even pIzzA.
There are currently two reserved variables names pi and e, which represent the numbers 3.14159265... and 2.7182818..., respectively.
Arithmetic
* | Multiplication |
/ | Division |
These are the 5 basic functions of arithmetic. Standard order of operations apply, i.e. Exponentiation, then multiplication and division, then addition and subtraction.
Exponentiation is right associative while the rest are left-associative. This means that x^y^z is the same as x^(y^z) while a+b+c is equivalent to (a+b)+c.
Trigonometric
sin | Sine |
cos | Cosine |
tan | Tangent |
csc | Cosecant |
sec | Secant |
cot | Cotangent |
asin | Arcsine |
acos | Arccosine |
atan | Arctangent |
acsc | Arccosecant |
asec | Arcsecant |
acot | Arccotangent |
These are the trignometric functions (and their inverses) found in any self-respecting pre-calculus textbook. Angles are always expressed in radians.
Hyperbolic Functions
sinh | Hyperbolic Sine |
cosh | Hyperbolic Cosine |
tanh | Hyperbolic Tangent |
csch | Hyperbolic Cosecant |
sech | Hyperbolic Secant |
coth | Hyperbolic Cotangent |
asinh | Hyperbolic ArcSine |
acosh | Hyperbolic ArcCosine |
atanh | Hyperbolic ArcTangent |
acsch | Hyperbolic ArcCosecant |
asech | Hyperbolic ArcSecant |
acoth | Hyperbolic ArcCotangent |
These are the hyperbolic functions (and their inverses) found in any self-respecting calculus textbook.
Sign Functions
- | Negation |
neg | Negation |
abs | Absolute Value |
sgn | Sign |
These are unary functions which deal with the sign of the given argument. The expressions -x and neg(x) are equivalent way to express the negation of x. The expression abs(x) is the absolute value of x. The expression sgn(x) is 1 if x>0, -1 if x<0, and 0 if x=0.
Roots
sqrt | Square Root |
root | nth Root |
sqrt is a unary function that evaluates the the square root of the argument.
root is a binary function that calculates the nth root. The general format is root(x, n), where n is an integer. This is preferred to x^(1/n) since you'll notice that if n is odd, the x^(1/n) is undefined for negative x.
Exponential/Logarithm
exp | Exponential |
log | Common Logarithm |
ln | Natural Logarithm |
logb | Log base b |
exp is a unary function that evaluates the the exponential of the argument. It is equivalent to e^x.
log and ln are unary functions that evaluate the the common and natural logarithm of the argument.
Finally, logb(x,b) evaluates the logarithm base b of x. It is mathematically equivalent to log(x)/log(b) and ln(x)/ln(b). Conversely log(x) and ln(x) are equivalent to logb(x,10) and logb(x,e), respectively.
Engineering
sqwave | Square Wave |
trwave | Triangle Wave |
swwave | Sawtooth Wave |
sqpulse | Square Pulse |
trpulse | Triangle Pulse |
swpulse | Sawtooth Pulse |
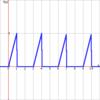
(Figure 1)
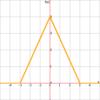
(Figure 2)
Each of the three wave functions (sqwave, trwave, and swwave) take three arguments. The general format is XXwave(t,d,T), where t is a time function, 0<d<1 is the duty cycle, and T is the period. For example,
sqwave(x,1/3,3)
will produce the graph shown (Figure 1).
Each of the three pulse functions (sqpulse, trpulse, and swpulse) take two arguments. The general format is XXpulse(t,a), where t is a time function. The pulse will 'turn on' at t=0 and 'turn off' at t=a. For example, 4 trpulse(t+3,6) will produce the graph shown (Figure 2).
Step function is also known as the Heavyside function. step(x) is 1 if x is positive, and 0 otherwise.
Finally the stair function stair(x,a) is 0 when x is negative. There is a rise of 1 (starting at x=0) and a run of a.
Rounding
The rounding function, ceil and floor are both unary functions which return a rounded value of the argument. ceil(x) is the smallest (closest to negative infinity) integer that is not greater than x. Similarly, floor(x) is the largest (closest to positive infinity) integer that is not less than x.
Maximum and Minimum
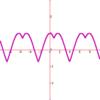
(Figure 3)
max and min are multi-ary functions which respectively compute the maximum and minimum of the given parameters. For example max(cos(x),sin(x)) will generate the graph shown (Figure 3). Both max and min can take many inputs.
Sum and Product
sum and prod are multi-ary functions which respectively compute the sum and product of the given parameters. For example sum(1,-2x,x^2) is equivalent to 1-2x+x^2. Both these functions can take many inputs.
Calculus
diff | Differentiation |
int | Numerical Integration |
taylor | Taylor Series Approximation |
diff has the format diff(f,x), where the first argument is a multivariable function. Differentiation is always with respect to some variable, which is named in the other argument of diff. One can also name multiple variables, to take multiple derivatives with respect to those variables. For example, diff(x^2 y^2, x, y) will be the same as 4x*y.
int has the general format int(f,x,a,b,tol), where
f is a function of one variable,
x is variable of integration,
a and b are the lower and upper end point, respectively, and
tol is the tolerance of the numerical integration algorithm.
GCalc utilizes an adaptive
Simpson's rule algorithm for numerical integration. Be careful when integrating nonsmooth or discontinuous functions.
Given a function f with independent variable x, the taylor polynomial approximation of f of degree n at x0 can be found with taylor(f,x0,n).
Equality/Inequality Operations
== | Equals |
<> | Not Equals |
>= | Greater than or equal |
> | Greater than |
<= | Less than or equal |
< | Less than |
These operations take two numbers and does a comparison. If the inequality or equality evaluates to true, then the operation returns 1. Otherwise, the operation returns a NaN (Not A Number).
Boolean Operations
not | Logical Negation ('not') |
&& | Conjunction ('and') |
|| | Disjunction ('or') |
These standard logical operation take inequalities or other boolean operations as arguments. The operation not is unary, while && and || are (infix) binary. For example,
not(x>1 && x<=y)
is a valid expression.
Be sure to use parentheses with not to minimize confusion about order of precedence.
Piecewise Function

(Figure 4)
With case, one can define a piecewise function. The general format is case(t1,v1,t2,v2,...,[default]). If the test tN evaluates to true, then the function value is the value vN at that point. At any given point, if multiple tests evaluate to true, then the function value is the value corresponding to the first test that evaluates to true. If no test evaluates to true, then either the function takes on the optional default or is undefined.
For example, case(x^2<=pi^2,sin(x),0) corresponds to the graph shown (Figure 4).




